The marginal likelihood of a model is one the key quantities appearing throughout machine learning and statistics, since it provides an intuitive and natural objective function for model selection and parameter estimation. I recently read a new paper by Sumio Watanabe on A Widely applicable Bayesian information criterion (WBIC)[cite key="watanabe2012widely"] (and to appear in JMLR soon) that provides a new, theoretically grounded and easy to implement method of approximating the marginal likelihood, which I will briefly describe in this post. I'll summarise some of the important aspects of the marginal likelihood and then briefly describe the WBIC and some thoughts and questions on its use.
The Marginal Likelihood
The marginal likelihood (or its log) goes by many names in the literature, including the model evidence, integrated likelihood, partition function, and Bayes' free energy, and is the likelihood function (a function of data and model parameters) averaged over the parameters with respect to their prior distribution. If we consider a model 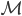 , a data set
, a data set 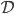 and model parameters
and model parameters 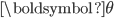 , then the marginal likelihood
, then the marginal likelihood 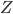 is:
is:
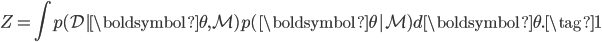
While this might be an uninteresting normalising constant if we were interested in inference or prediction, the marginal likelihood has the nice interpretation as a measure of how likely the data is to have been generated from the model. In particular, we can use it to look at the support for a model given the data. Considering a prior over a model 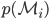 . We get the posterior over the model using Bayes' theorem:
. We get the posterior over the model using Bayes' theorem: 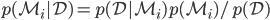 . To compare two models, we could then look at the posterior odds of the two models (and assuming models are equally probable a priori), we come to the popular Bayes' factor
. To compare two models, we could then look at the posterior odds of the two models (and assuming models are equally probable a priori), we come to the popular Bayes' factor 
- Consistency: As the number of data points becomes large, it will favour the true model.
- Ockham's razor: We will prefer simpler models to more complex ones if they have the same performance.
- Comparison: Models and parameters that are compared need not be nested or equivalent in any way.
- Reference: We can store the marginal likelihood as a property of the model-data instance, and use it for any future model selection or comparison.
- Weight-of-evidence: We can compute the evidence for data points individually and use this as a score or measure of surprise, allowing us to characterise each data point we observe.
Computing the Marginal Likelihood
Of course, this requires the integral eq. (1) to be computed and is typically intractable (due to non-conjugacy, high dimensionality, large amounts of data). But many approaches exist for its computation. I would group the available approaches into three types, and I list the methods I have some experience with here.
Stochastic Methods
- Harmonic mean estimator. Not suggested, unstable and high variance.
- Chib's estimator [cite key="chib1995marginal"]. A good estimator for simpler models, since it relies only on the output of a Gibbs sampler. Will not give good results for models where good mixing of the Markov chain is hard to obtain.
- Annealed importance sampling [cite key="neal2001annealed"] (and closely related thermodynamic integration). Currently, one of the best ways of computing to the 'true' marginal likelihood, but takes a very long time. It is difficult to know what makes a good annealing schedule and difficult to tune the large number of Markov chains that will be simulated.
Deterministic Approximations
- Variational lower bounds [cite key="wainwright2008graphical"]. Very accurate for many problems and scalable. Useful in that we obtain a lower bound on the marginal likelihood and are applicable to broad classes of models (e.g., regression models, factor models). Limited by ability to obtain a good lower bound, especially when (local) lower bounds must be introduced (to compute required expectations), in addition to the initial use of of Jensen's inequality.
- Expectation propagation approximations [cite key="minka2001expectation"]. Very accurate for many problems and scalable, but limited by the ability to compute moments of high dimensional distributions (e.g., categorical data) and not generally applicable (e.g., factor models).
Large-sample Approximations
- Akaike informtion criterion (AIC), Bayesian information criterion (BIC) or Schwartz criterion or Minimum description length (MDL), Deviance information criterion (DIC), and Laplace approximations. These methods rely on normal asymptotic approximations of the marginal likelihood. For models where this holds, these estimates are easy to compute and accurate. For many models with latent variables and missing values this will not be the case and we'll get unreliable estimates.
Widely Applicable Bayesian Information Criterion (WBIC)
Watanabe [cite key="watanabe2012widely"] proposed a new method for estimating the marginal likelihood, falling in the class of large-sample approximations. The widely applicable Bayesian information criterion (WBIC) is applicable to models with latent variables or hierarchical structure, such as neural networks, hidden Markov models, mixture models and factor regression models. In its simplest form, for a data set with N observations, the WBIC is computed using the following algorithm:
- Set temperature
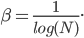
- Generate T samples from an annealed distribution at temperature
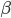 :
: 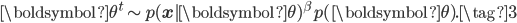
- Compute
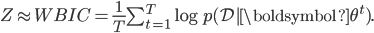
To make use of WBIC, we need the asymptotic condition that  is sufficiently small. Samples from the annealed distribution can be generated using MCMC methods like hybrid (Hamiltonian) Monte Carlo or by slice sampling. This has the advantage that their is only one temperature value needed, and only one Markov chain that needs to be simulated.
is sufficiently small. Samples from the annealed distribution can be generated using MCMC methods like hybrid (Hamiltonian) Monte Carlo or by slice sampling. This has the advantage that their is only one temperature value needed, and only one Markov chain that needs to be simulated.
There is a nice connection to thermodynamic integration and annealed importance sampling (AIS). For these methods, we need to generate samples from annealed distributions of the form eq. (3) for a sequence 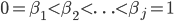 . WBIC shows that in some problems only a single
. WBIC shows that in some problems only a single 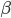 is needed when using an asymptotic approximation, which reduces the computational burden significantly. But, it is here that the technical conditions of the paper play a role. The algorithm as I described is for models that have a 'parity' of 0 or 1, a concept introduced in the paper. From much of the recent work in this area and my communication with S. Watanabe, the ability to determine this 'parity' is difficult for many models (though this is known for some models, e.g., reduced rank regression). Where the parity for a model is unknown, we must then search for the optimal
is needed when using an asymptotic approximation, which reduces the computational burden significantly. But, it is here that the technical conditions of the paper play a role. The algorithm as I described is for models that have a 'parity' of 0 or 1, a concept introduced in the paper. From much of the recent work in this area and my communication with S. Watanabe, the ability to determine this 'parity' is difficult for many models (though this is known for some models, e.g., reduced rank regression). Where the parity for a model is unknown, we must then search for the optimal 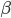 . Much is known about the optimal form of
. Much is known about the optimal form of 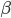 but it depends on other unknown quantities, making its search difficult.
but it depends on other unknown quantities, making its search difficult.
In a subsequent post I'll look at some comparisons of these various methods for marginal likelihood estimation. At present the WBIC is an intriguing idea allowing us to use algebraic geometry for statistical problems. Hopefully more will come soon expanding on this work allowing us to understand when it can be applied sensibly. My own feeling is to rely on deterministic approximations or sampling methods until then. There are also a few additional comments and links to related papers for WBIC listed on Watanabe's webpage.
[bibsource file=http://www.shakirm.com/blog-bib/marginal-likelihood-wbic.bib]
Nice post. I would love to see an update on this!
Great introduction to WBIC. Looking forward to follow-up comments.
Thanks,
Tom Aldenberg