Throughout this series, we have discussed deep networks by examining prototypical instances of these models, e.g., deep feed-forward networks, deep auto-encoders, deep generative models, but have not yet interrogated the key word we have been using. We have not posed the question what does 'deep' mean, and what makes a model deep. There is little in way of a detailed discussion as to what constitutes a 'deep' model and can be hard to do — it seems appropriate as a closing attempt to provide one such view.
Arguably, deep learning today means much more than a description of a class of useful models. It espouses the use of powerful non-linear models, models that provide unified loss functions that allow for end-to-end training, machine learning approaches designed from the beginning to be scalable and amenable to large data sets, and to computational methods that fully exploit modern computing resources. While these other factors have been most remarkably demonstrated with deep learning, these are goals shared with all other areas of machine learning. What is of central importance is 'deep' as a characterisation of models and their desirable features.
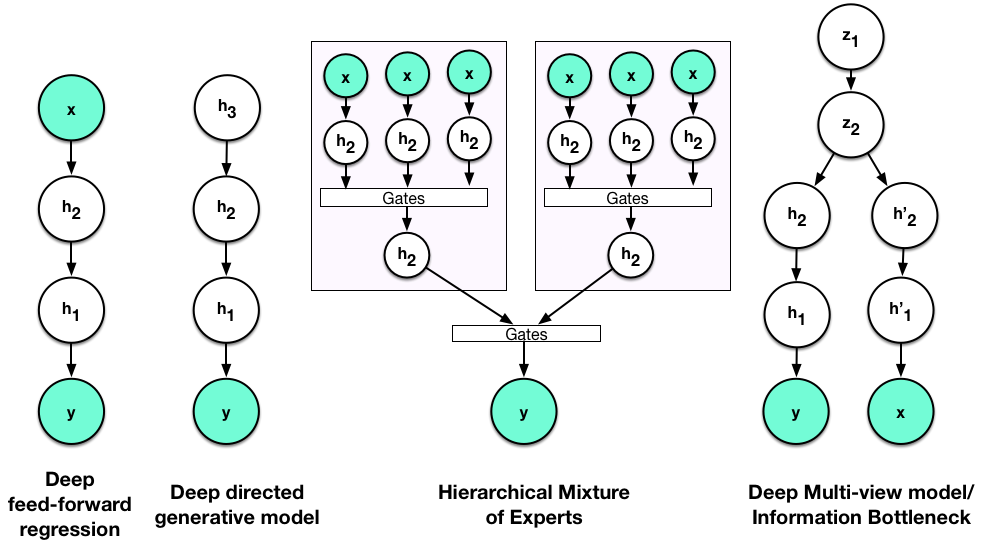
Deep and Hierarchical Models
If we look into the existing literature, deep learning is generally described as the machine learning of deep models. And a deep model is any model that involves multiple levels of computation, in particular, computation achieved by the repeated application of non-linear transformations [cite key="bengio2009learning"] . This is a general framework and the number of transformations used forms the depth of the model. This is well-suited as a description of neural networks (or recursive GLMs), since we can easily construct a model by recursively applying a linear transformation followed by an element-wise non-linearity, allowing us to move from linear regression models that use only one (non-)linear transformation (so called 'shallow' models) to more complex non-linear regressions that use three or more non-linear transformations (i.e. 'deep' models).
To provide a statistical view, we need a slightly more precise framework — and will use that of hierarchical models. As a start, we will characterise deep feed-forward models and then generalise from this type of model. Feed-forward networks are constructed from a succession of non-linear transformations that form a mapping from inputs x to targets y with parameters 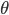 . Representing each transformation using a 'layer'
. Representing each transformation using a 'layer' 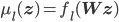 , the final output is obtained by the composition of layers:
, the final output is obtained by the composition of layers:
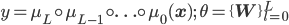
For sigmoidal networks, the activation function f is a sigmoid function. We were previously able to recast this model as a general probabilistic regression model 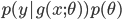 , corresponding to a familiar regularised deep neural network whose loss, with regulariser
, corresponding to a familiar regularised deep neural network whose loss, with regulariser 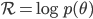 , is:
, is:
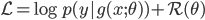
As a probabilistic model, we could instead think of the output of every layer 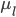 as a random (latent) variable, with the property that the expectation of a layer is given by the non-linear transformation, and the sequence of expectations producing the output:
as a random (latent) variable, with the property that the expectation of a layer is given by the non-linear transformation, and the sequence of expectations producing the output:
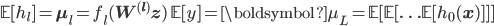
It is this characterisation that brings us to hierarchical models: models where its (prior) probability distributions can be decomposed into a sequence of conditional distributions [cite key="robert2007bayesian"][Ch. 10]:
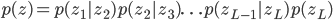
This specification implies that the prior is composed of a sequence of stochastic computations, and satisfies the aspirations we established for deep models. A hierarchical construction is not restricted to regression and is a general framework for all models, including density estimation, time-series models, spatial statistics, etc. Our sigmoidal networks can instead be written as the following hierarchical regression model:
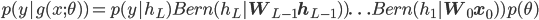
At layer l, the inputs from the previous layer  are transformed using a linear mapping into natural parameters of the Bernoulli distribution (into the pre-synaptic activations). Since we perform maximum likelihood estimation in the canonical or mean parameters of this model, there is an implicit transformation of the natural parameters using a sigmoid function — a link function for the Bernoulli distribution.
are transformed using a linear mapping into natural parameters of the Bernoulli distribution (into the pre-synaptic activations). Since we perform maximum likelihood estimation in the canonical or mean parameters of this model, there is an implicit transformation of the natural parameters using a sigmoid function — a link function for the Bernoulli distribution.
The conclusion from this is that one way to view deep feed-forward networks are as hierarchical probabilistic models. What is important though, is that this hierarchy is a hierarchy formed through the means of the layer-distributions. Only the mean parameters at every layer of the hierarchy depend on computations from previous parts of the hierarchy, i.e. hierarchies whose dependency is through the first-order structure at every layer of the model.
Characterising Deep Models
Almost all models we use in deep learning are models formed through hierarchies of the mean. Deep generative models are another popular model class with this characteristic. One widely-known example is a Sigmoid belief network (SBN), a deep directed graphical models with Bernoulli latent variables. The hierarchical formulation through the means is:
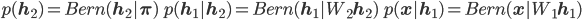
- Non-linear Gaussian belief networks (NLGBNs) follow the same hierarchy as SBNs, but use Gaussian latent variables, and form the hierarchy through the Gaussian means. And is closely related to hierarchical ICA.
- Deep Latent Gaussian Models (DLGMs)[cite key=rezende2014stochastic] and Deep Auto-regressive Networks (DARN)[cite key=gregor2013deep] form their hierarchy through the means of Gaussian and auto-regressive Bernoulli distributions, respectively.
- Deep Gaussian Processes, a non-parametric analog of the NLGBNs, are formed through a hierarchical dependency through its mean functions.
- Deep Exponential Families (DEF), similar to the description above for deep feed-forward networks, construct a hierarchical model using one-parameter exponential families. This single (canonical) parameter controls all moments of the distribution and often directly encodes the mean, so any hierarchy formed in this way is a hierarchical model of the means.
- Deep Boltzmann Machines (DBM) are graphical undirected models (i.e. all conditional probabilities and restrictions are fully specified by its graphical depiction) also form hierarchical log-linear models using one-parameter exponential families.
The intuition we obtain from deep learning is that every stage of computation, every non-linear transformation, allows us to form increasingly abstract representations of the data. Statistically, every hidden layer allows us to capture more long-range and higher order correlations in the data (after being integrated out). In either view, these hierarchies are important since they provide a highly efficient way to construct complex models, e.g., in a mixture model we can use a 2-layer hierarchy using K and L clusters at each layer, effectively modelling 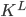 clusters — something infeasible with a standard (flat) mixture model. Parts of our hierarchy far away from the data are indeed more abstract (diffuse and close to the prior), since they have a small effect on the data distribution: this implies that to effectively learn with and use deep models, we require large amounts of data.
clusters — something infeasible with a standard (flat) mixture model. Parts of our hierarchy far away from the data are indeed more abstract (diffuse and close to the prior), since they have a small effect on the data distribution: this implies that to effectively learn with and use deep models, we require large amounts of data.
Beyond Hierarchies of the Mean
Deep models forming their hierarchies through the mean parameters are amongst the most powerful and flexible models in the machine learning toolbox. If you are going to build any hierarchical model, a hierarchy through the mean is a very good idea indeed. There are two aspects that follow from this: firstly, there are many models that are formed through mean-hierarchies that are not labelled as deep; secondly, a hierarchy through the mean represents just one way to build such a hierarchical model.
There are many other interesting models that are formed through hierarchical constructions, and some include:
- Hierarchies on variances: this is a natural step and is used in many Bayesian models where learning variances is involved. This does raise interesting research questions as to what assumptions and distributions to use beyond the simple one-parameter exponential families that are widely used.
- Hierarchical mixture models, mixed-membership models and admixture models: These models form a mixture of mixture-models. These are not typically called deep, though they could be called that. As mentioned above, we can easily can represent
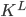 mixture components using such constructions. They show how different representations can be combined in useful ways, e.g., if the mixture is over deep feed-forward networks.
mixture components using such constructions. They show how different representations can be combined in useful ways, e.g., if the mixture is over deep feed-forward networks. - And some other interesting instances:
- Bayesian networks and multi-level regression models.
- Hierarchical Dirichlet processes.
- As Wray Buntine points out (see comment below) these are also hierarchical models of the mean, and points to another aspect that has not been discussed: that of distributed representations. Deep learning emphasises distributed representations (using multivariate continuous latent variables), and models such as the HDP show how both distributed and partitioned representations can be used together to provide powerful and adaptive models.
- Canonical Correlation, Information Bottleneck and multi-view models.
- Multi-level spike-and-slab models.
Summary
One way to characterise models described as deep are as hierarchical models of means: hierarchical models where the mean at every layer of the hierarchy depends on computation in previous parts of the hierarchy. This is a correspondence we find in almost all models characterised as deep in our current practice, whether these be deep neural networks, deep latent Gaussian models, deep exponential families or deep Gaussian processes. This is always our first approach in building modern machine learning models, since we can capture a great deal of the structure underlying our data in this way. But we also know how to extend our hierarchies in ways that allow us to specify other structural aspects we may be interested in. While it is conceptually easy to extend our hierarchies in many ways, techniques for dealing with hierarchies other than the mean in computationally efficient ways are still missing, and remains one of the important research questions that we face in machine learning.
This forms last post I've planned in this series and plan to post a brief summary of the set as a follow-up. Plans and thoughts are underfoot for a new set of musings (in reinforcement learning or neuroscience).
[bibsource file=http://www.shakirm.com/blog-bib/SVDL6.bib]
Technically, hierarchical Dirichlet processes and hierarchical Pitman-Yor processes are also hierarchies of the mean. They also have fast algorithms which *some* of us use, and *some* have parallelised.
"While it is conceptually easy to extend our hierarchies in many ways, techniques for dealing with hierarchies other than the mean in computationally efficient ways are still missing"
One way to do it is with massively parallel computer chip architectures where data can be streamed through, each layer working on new raw or preprocessed data simultaneously. But the biggest gains will be when the von Neumann bottleneck is removed and energy and time won't be wasted shuttling data around. Check out AHaH Computing for one such example utilizing memristors: http://knowm.org/ahah-computing/