With the success of discriminative modelling using deep feedforward neural networks (or using an alternative statistical lens, recursive generalised linear models) in numerous industrial applications, there is an increased drive to produce similar outcomes with unsupervised learning. In this post, I'd like to explore the connections between denoising auto-encoders as a leading approach for unsupervised learning in deep learning, and density estimation in statistics. The statistical view I'll explore casts learning in denoising auto-encoders as that of inference in latent factor (density) models. Such a connection has a number of useful benefits and implications for our machine learning practice.
Generalised Denoising Auto-encoders
Denoising auto-encoders are an important advancement in unsupervised deep learning, especially in moving towards scalable and robust representations of data. For every data point y, denoising auto-encoders begin by creating a perturbed version of it y', using a known corruption process
![]()
. We then create a network that given the perturbed data y', reconstructs the original data y. The network is grouped into two parts, an encoder and a decoder, such that the output of the encoder z can be used as a representation/features of the data. The objective function is [cite key =vincent2008extracting]:
![]()
![]()
![]()
where
![]()
is an appropriate likelihood function for the data, and the objective function is averaged over all observations. Generalised denoising auto-encoders (GDAEs) realise that this formulation may be limited due to finite training data, and introduce an additional penalty term
![]()
for added regularisation [cite key=bengio2013generalized]:
![]()
GDAEs exploit the insight that perturbations in the observation space give rise to robustness and insensitivity in the representation z. Two key questions that arise when we use GDAEs are: how to choose a realistic corruption process, and what are appropriate regularisation functions.
Separating Model and Inference
The difficulty in reasoning statistically about auto-encoders is that they do not maintain or encourage a distinction between a model of the data (statistical assumptions about the properties and structure we expect) and the approach for inference/estimation in that model (the ways in which we link the observed data to our modelling assumptions). The auto-encoder framework provides a computational pipeline, but not a statistical explanation, since to explain the data (which must be an outcome of our model), you must know it beforehand and use it as an input. Not maintaining the distinction between model and inference impedes our ability to correctly evaluate and compare competing approaches for a problem, leaves us unaware of relevant approaches in related literatures that could provide useful insight, and makes it difficult for us to provide the guidance that allows our insights to be incorporated into our community's broader knowledge-base.
To ameliorate these concerns we typically re-interpret the auto-encoder by seeing the decoder as the statistical model of interest (and is indeed how many interpret and use auto-encoders in practice). A probabilistic decoder provides a generative description of the data, and our task is inference/learning in this model. For a given model, there are many competing approaches for inference, such as maximum likelihood (ML) and maximum a posteriori (MAP) estimation, noise-contrastive estimation, Markov chain Monte Carlo (MCMC), variational inference, cavity methods, integrated nested Laplace approximations (INLA), etc. The role of the encoder is now clear: the encoder is one mechanism for inference in the model described by the decoder. Its structure is not tied to the model (decoder), and it is just one from the smorgasbord of available approaches with its own advantages and tradeoffs.
Approximate Inference in Latent Variable Models
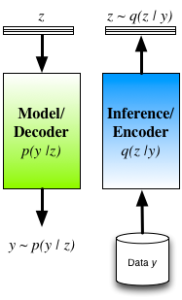
Another difficulty with DAEs is that robustness is obtained by considering perturbations in the data space — such a corruption process will, in general, not be easy to design. Furthermore, by carefully reasoning about the induced probabilities, we can show [cite key="vincent2008extracting"] that the DAE objective function
![]()
corresponds to a lower bound obtained by applying the variational principle to the log-density of the corrupted data
![]()
— this though, is not a quantity we are interested in reasoning about.
A way forward would be to instead apply the variational principle to the quantity we are interested in, the log-marginal probability of the observed data
![]()
[cite key="rezende2014stochastic"][cite key="kingma2013auto"]. The objective function obtained by applying the variational principle to the generative model (probabilistic decoder) is known as the variational free energy:
![]()
By inspection, we can see that this matches the form of the GDAE objective. There are notable differences though:
- Instead of considering perturbations in the observation space, we consider perturbations in the hidden space, obtained by using a prior p(z). The hidden variables are now random, latent variables. Auto-encoders are now generative models that are straightforward to sample from.
- The encoder q(z|y) is a mechanism for approximating the true posterior distribution of the latent/hidden variables p(z|y).
- We are now able to explain the introduction of the penalty function in the GDAE objective in a principled manner. Rather than designing the penalty by hand, we are able to derive the form this penalty should take, appearing as the KL divergence between the the prior and the encoder distribution.
Auto-encoders reformulated in this way, thus provide an efficient way of implementing approximate Bayesian inference. Using an encoder-decoder structure, we gain the ability to jointly optimise all parameters using the single computational graph; and we obtain an efficient way of doing inference at test time, since we only need a single forward pass through the encoder. The cost of taking this approach is that we have now obtained a potentially harder optimisation, since we have coupled the inferences for the latent variables together through the parameters of the encoder. Approaches that do not implement the q-distribution as an encoder have the ability to deal with arbitrary missingness patterns in the observed data and we lose this ability, since the encoder must be trained knowing the missingness pattern it will encounter. One way we explored these connections is in a model we called Deep Latent Gaussian Models (DLGM) with inference based on stochastic variational inference (and implemented using an encoder) [cite key="rezende2014stochastic"], and is now the basis of a number of extensions [cite key="kingma2014semi"][cite key="gregor2015draw"].
Summary
Auto-encoders address the problem of statistical inference and provide a powerful mechanism for inference that plays a central role in our search for more powerful unsupervised learning. A statistical view, and variational reformulation, of auto-encoders allows us to maintain a clear distinction between the assumed statistical model and our approach for inference, gives us one efficient way of implementing inference, gives us an easy-to-sample generative model, allows us to reason about the statistical quantity we are actually interested in, and gives us a principled loss function that includes the important regularisation terms. This is just one perspective that is becoming increasingly popular, and is worthwhile to reflect upon as we continue to explore the frontiers of unsupervised learning.
[bibsource file=http://www.shakirm.com/blog-bib/aeVInf.bib]
Nice post :)))
I'm coding up the DRAW paper at the moment. It's interesting that the attention mechanism, contributes to the reconstruction loss through the write operation controlled by the decoders hidden layer. The read operation contributes to the latent loss through the statistics mu_t and sigma_t of the approximate posterior which are linear transforms of the encoders hidden layer.
There's a beautiful symmetry of using the encoder RNN to control where in the data to infer the latent model, and the decoder RNN to generate the parametric model of the data.
As usual the only way to understand it is to code it, but its definitely worth the effort!