Machine learning involves manipulating probabilities. These probabilities are most often represented as normalised-probabilities or as log-probabilities. An ability to shrewdly alternate between these two representations is a vital step towards strengthening the probabilistic dexterity we need to solve modern machine learning problems. Today's trick, the log derivative trick, helps us to do just this, using the property of the derivative of the logarithm. This trick shines when we use it to solve stochastic optimisation problems, which we explored previously, and will give us a new way to derive stochastic gradient estimators. We begin by using the trick to define the score function, a function we have all used before, even if not under that name.
Score Functions
The log derivative trick is the application of the rule for the gradient with respect to parameters ![]() of the logarithm of a function
of the logarithm of a function ![]() :
:
![]()
The significance of this trick is realised when the function ![]() is a likelihood function, i.e. a function of parameters
is a likelihood function, i.e. a function of parameters ![]() that provides the probability of a random variable x. In this special case, the function
that provides the probability of a random variable x. In this special case, the function ![]() is called a score function, and the right-hand side is the score ratio. The score function has a number of useful properties:
is called a score function, and the right-hand side is the score ratio. The score function has a number of useful properties:
- The central computation for maximum likelihood estimation. Maximum likelihood is one of the dominant learning principles used in machine learning, used in generalised linear regression, deep learning, kernel machines, dimensionality reduction, and tensor decompositions, amongst many others, and the score appears in all these problems.
- The expected value of the score is zero. Our first use of the log-derivative trick will be to show this.
![]()
![]()
In the first line we applied the log derivative trick and in the second line we exchanged the order of differentiation and integration. This identity is the type of probabilistic flexibility we seek: it allows us to subtract any term from the score that has zero expectation, and this modification will leave the expected score unaffected (see control variates later).
- The variance of the score is the Fisher information and is used to determine the Cramer-Rao lower bound.
![]()
We can now leap in a single bound from gradients of a log-probability to gradients of a probability, and back. But the villain of today's post is the troublesome expectation-gradient of Trick 4, re-emerged. We can use our new-found power—the score function—to develop yet another clever estimator for this class of problems.
Score Function Estimators
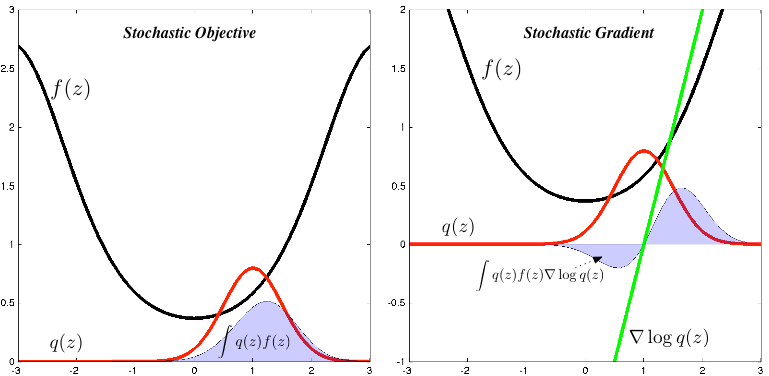
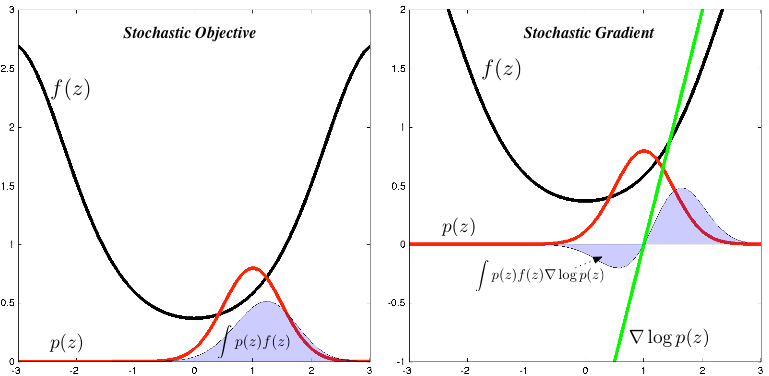
Our problem is to compute the gradient of an expectation of a function f:
![]()
This is a recurring task in machine learning, needed for posterior computation in variational inference, value function and policy learning in reinforcement learning, derivative pricing in computational finance, and inventory control in operations research, amongst many others.
This gradient is difficult to compute because the integral is typically unknown and the parameters ![]() , with respect to which we are computing the gradient, are of the distribution
, with respect to which we are computing the gradient, are of the distribution ![]() . Furthermore, we might want to compute this gradient when the function f is not differentiable. Using the log derivative trick and the properties of the score function, we can compute this gradient in a more amenable way:
. Furthermore, we might want to compute this gradient when the function f is not differentiable. Using the log derivative trick and the properties of the score function, we can compute this gradient in a more amenable way:
![]()
Let's derive this expression and explore the implications of it for our optimisation problem. To do this, we are will use one other ubiquitous trick, a probabilistic identity trick, where we multiply our expressions by 1—a one formed by the division of a probability density by itself. Combining the identity trick with the log-derivative trick, we obtain a score function estimator for the gradient:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\approx \frac{1}{S} \sum_{s=1}^{S}f(z^{(s)})\nabla_\theta \log p(z^{(s)};\theta) \quad z^{(s)}\sim p(z)\]](https://blog.shakirm.com/wp-content/ql-cache/quicklatex.com-eeb12082734b75280ec7761e6667d474_l3.png)
A lot has happened in these four lines. In the first line we exchanged the derivative and the integral. In the second line, we applied our probabilistic identity trick, which allowed us to form the score ratio. Using the log-derivative trick, we then replaced this ratio with the gradient of the log-probability in the third line. This gives us our desired stochastic estimator in the fourth line, which we computed by Monte Carlo by first drawing samples from p(z) and then computing the weighted gradient term.
This is an unbiased estimator of the gradient. Our assumptions throughout this process have been simple:
- The exchange of integration and differentiation is valid. This is hard to show in general, but will rarely be a problem. We can reason about the correctness of this by appealing to the Leibniz integral rule and the available analysis [cite key=l1993interchange].
- The function f(z) need not be differentiable. Instead, we should be able to evaluate it or observe its value for a given z.
- Obtaining samples from the distribution p(z) is easy, since this is needed for Monte Carlo evaluation of the integral.
Like so many of our tricks, the path we have taken has been trodden upon by many other research areas, each sharing the tale of their adventure with a name related to their problem formulation. These include:
- Score function estimators
- Our derivation allowed us to transform the gradient of an expectation into a an expectation of a score function
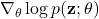 making it natural to refer to such estimators as score function estimators [cite key=kleijnen1996optimization]. This is a common usage, and my preferred one.
making it natural to refer to such estimators as score function estimators [cite key=kleijnen1996optimization]. This is a common usage, and my preferred one.
- Optimization and sensitivity analysis of computer simulation models by the score function method, is insightful and describes many important historical developments.
- Our derivation allowed us to transform the gradient of an expectation into a an expectation of a score function
- Likelihood ratio methods
- P. W. Glynn has been amongst the most influential in popularising this class of estimator. Glynn [cite key=glynn1990likelihood] interpreted the score ratio
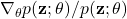 as a likelihood ratio, and describes the estimators as likelihood ratio methods. I think this is a slightly non-standard use of the term likelihood ratio—likelihood ratios typically represent the ratio of the same function under different parameter settings, rather than a ratio of different functions under the same parameter setting—hence my preference for the name score function estimators. Many authors such as Fu [cite key=fu2006gradient] refer instead to likelihood ratio/score function (LR/SF) methods. Important papers:
as a likelihood ratio, and describes the estimators as likelihood ratio methods. I think this is a slightly non-standard use of the term likelihood ratio—likelihood ratios typically represent the ratio of the same function under different parameter settings, rather than a ratio of different functions under the same parameter setting—hence my preference for the name score function estimators. Many authors such as Fu [cite key=fu2006gradient] refer instead to likelihood ratio/score function (LR/SF) methods. Important papers:
- 'Likelihood Ratio Gradient Estimation for Stochastic Systems', by Glynn is detailed and explains the important variance properties
- Gradient Estimation by Michael Fu is indispensable.
- P. W. Glynn has been amongst the most influential in popularising this class of estimator. Glynn [cite key=glynn1990likelihood] interpreted the score ratio
- Automated Variational Inference
- Variational inference transforms intractable integrals appearing in Bayesian analysis into stochastic optimisation problems. It is no surprise then that score function estimators also appear in this area, and under many different names: variational stochastic search, automated variational inference, black-box variational inference and neural variational inference, are just the few I know of.
- REINFORCE and policy gradients
- For reinforcement learning problems, we can map the function f to the reward obtained from the environment, the distribution
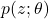 to the policy, and the score to the policy gradient (or sometimes the characteristic eligibility). An intuitive explanation then follows: any gradients of the policy that correspond to high rewards are weighted higher—reinforced—by the estimator. Hence, the estimator was called REINFORCE [cite key=williams1992simple], and its generalisation now forms the policy gradient theorem.
to the policy, and the score to the policy gradient (or sometimes the characteristic eligibility). An intuitive explanation then follows: any gradients of the policy that correspond to high rewards are weighted higher—reinforced—by the estimator. Hence, the estimator was called REINFORCE [cite key=williams1992simple], and its generalisation now forms the policy gradient theorem.
- For reinforcement learning problems, we can map the function f to the reward obtained from the environment, the distribution
Control Variates
To make this Monte Carlo estimator effective, we must ensure that its variance is as low as possible – the gradient will not be useful otherwise. To give us more control over the variance, we use the modified estimator:
![]()
where the new term ![]() is called a control variate, which are widely used for variance reduction in Monte Carlo estimators. A control variate is any term that we introduce to the estimator that has zero mean. They can thus always be introduced since they do not affect the expectation; control variates do affect the variance. The choice of control variate is the principal challenge in the use of score function estimators. The simplest method is to use a constant baseline, but other methods can use be used, such as clever sampling schemes (e.g., antithetic or stratified), delta methods, or adaptive baselines. This book by Glasserman [cite key=glasserman2003monte] provides one of the most comprehensive discussions of the sources of variance and techniques for variance reduction.
is called a control variate, which are widely used for variance reduction in Monte Carlo estimators. A control variate is any term that we introduce to the estimator that has zero mean. They can thus always be introduced since they do not affect the expectation; control variates do affect the variance. The choice of control variate is the principal challenge in the use of score function estimators. The simplest method is to use a constant baseline, but other methods can use be used, such as clever sampling schemes (e.g., antithetic or stratified), delta methods, or adaptive baselines. This book by Glasserman [cite key=glasserman2003monte] provides one of the most comprehensive discussions of the sources of variance and techniques for variance reduction.
Families of Stochastic Estimators
Contrast today's estimator with the one we derived using the pathwise derivative approach in trick 4.
![]()
![]()
We effectively have two approaches available to us, we can:
- differentiate the function f, using pathwise derivatives, if it is differentiable; or
- differentiate the density p(z), using the score function.
There are other ways to develop stochastic gradient estimators, but these two are the most general. They can be easily combined, allowing us to use the most appropriate estimator (that provides for the lowest variance) at different parts of our computation. Using a stochastic computational graph provides one framework for achieving this.
Summary
The log derivative trick allows us to alternate between normalised probability and log-probability representations of distributions. It forms the basis of the definition of the score function, and is subsequently what enables maximum likelihood estimation and the important asymptotic analysis that has shaped much of our statistical understanding. Importantly, we can use this to provide a general purpose gradient estimator for stochastic optimisation problems that forms the basis of many of the most significant machine learning problems we currently face. Monte Carlo gradient estimators are needed for the truly general-purpose machine learning we aspire to, making an understanding of them, and the tricks upon which they are built, essential.
[bibsource file=http://www.shakirm.com/blog-bib/trickOfTheDay/logDerivTrick.bib]
Greeeat one!!
Here I have quick question, if we use score function estimator using "control variate" to reduce variance, then we have to know the gradient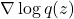 for each sample, since we need to evaluate the cov(f,h) and var(h) on a small batch of samples.
for each sample, since we need to evaluate the cov(f,h) and var(h) on a small batch of samples.
The issue here is that, if we want to draw multiple samples at once as a mini-batch, many autograd frameworks (such as PyTorch) cannot tell us the gradient for each sample, they just tell us the ACCUMULATED gradient, and because of this issue, I think we often cannot use mini-batch mode, instead we have to manually do a for-loop kinda thing doing ONE sample at a time, which would be too slow (at least I think so).
What do you think and suggest?
What an excellent blog - keep them coming!
"Furthermore, we might want to compute this gradient when the function f is not differentiable."
Hello, I have a question about the above sentence. I don't know why whether f is differentiable matters. Since f is not a function of theta, I think f is just a coefficient for the gradient.
Your posts are simply wonderful. Please keep writing. 🙂
Thank you.
"The is hard to show ..." -> "This is hard to show ..."
Great references! I'm partial to the term score function estimator for these methods as well. Another note: score function estimators also appear quite often in Monte Carlo methods and optimal transport theory. For example, one draws samples from the prior, and posits a path (or "transport", or "annealing") to the posterior; the path's rate of change is estimated using this score function approach. See, e.g., [1], as well as [2] for a more recent use case.
[1] Andrew Gelman and Xiao-Li Meng. https://projecteuclid.org/euclid.ss/1028905934
[2] Jeremy Heng, Arnaud Doucet, and Yvo Pokern. http://arxiv.org/abs/1509.08787