· Read in 10 minutes · 1700 words · collected posts ·
[dropcap]The[/dropcap] functioning of our brains, much like the intrigue of a political drama, is a neuronal house-of-cards. The halls of cognitive power are run by recurring alliances of neurons that deliberately conspire to control information processing and decision making. 'Suspicious coincidences' in neural activation—as the celebrated neuroscientist Horace Barlow observed—are abound; transparency in neural decision-making is needed. Barlow sought a deeper understanding of these processes, and to provoke debate, tabled five dogma of neural information processing [cite key=barlow1972single]. Of these dogma, Barlow's second proclaimed that the neuronal system is 'organised to achieve as complete a representation as possible with the minimum number of active neurons'. This is an elegant explanation of observed neural coincidences and provides a seemingly powerful neural processing strategy. But can such a strategy be justified?
Both brains and machines require clever ways in which to represent information and decisions. Not just any representation will do: many will be overly-complex and not simplify decision-making, others will require too much energy, and others may obstruct memory formation. Barlow alludes to the sparse use of neurons as a solution to the problem of efficient information representation, where only a small number of available neurons are used, and have been observed in many brain regions. The study of neural coincidences is known as sparse coding and is a computational principle that is successfully exploited by both brains and machines. This post is a brief exploration of the neuroscience and mathematics of learning with sparsity.
Sparse Sensory Representations
[dropcap]Sensory[/dropcap] data bombards the brain continuously. In order for the brain to perform the astounding variety of tasks that it is capable of, this sensory data must be analysed, synthesised and transformed into meaningful forms that support learning and decision making. The computational question we face, again following the framework of Marr's levels of analysis used in the previous post, is: how are meaningful representations of sensory data formed and used in the brain?
To answer this question, modern neuroscience has developed an array of tools to record how neurons are activated and used in the brain. These tools include: whole-cell patch-clamp recordings, sharp-electrode recordings, tetrode and juxtacellular recordings, calcium imaging, antidromic stimulation, and functional magnetic resonance imaging. These tools provide a rich implementation level understanding of neural firing and where sparse activations are used.
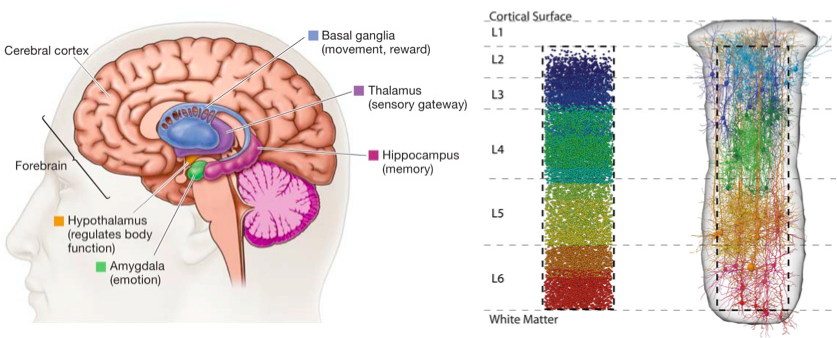
To appreciate the widespread use of sparse representations, imagine a tour that descends through a cortical column (see figure). A cortical column represents a functional unit of the cerebral cortex, consisting of 6 layers. Layer 4 in this hierarchy divides the supragranular layers close to the cortical surface (layers 1-3) from the deeper infragranular layers (layers 5 and 6). The tour begins with the supragranular layers, where imaging studies show that there is a high degree of sparse neural activation in layers 2 and 3, although the proportion of active neurons has been hard to establish (ranging from 20%-50% depending on the organism, brain region and measurement technique used). The infragranular layers are less sparse, but conclusions are limited by a lack of evidence since recording is hard due to their depth. Layer 4 is where the majority of inputs from the thalamus are connected. The firing of thalamic neurons is weak and requires many thalamic neurons to fire in order to activate neurons in layer 4, resulting in a sparsity of 50% or more [cite key=barth2012experimental]. As another mechanism that promotes sparsity, a single thalamic neuron connects to many layer 4 neurons—an overcomplete representation. Overcompleteness and sparsity is also seen in the connections of layer 2/3 neurons to higher layers [cite key=olshausen2004sparse].
We have accumulated evidence for the sparse use of neurons across the animal kingdom, over many brain regions, and verified by multiple measurement techniques; evidence in [cite key=barth2012experimental][cite key= olshausen2004sparse][cite key=hulme2014sparse][cite key= foldiak1995sparse]:
- Visual cortex of primates,
- Auditory system of rats,
- Somatosensory cortex of rats,
- Olfactory system of insects,
- Motor cortex of rabbits,
- Higher vocal centre of songbirds,
- Prefrontal cortex of rhesus monkeys,
- Hippocampus of rats, macaques and humans.
Barlow's second dogma is now transformed into the sparse coding hypothesis stating that 'sparse representations constitute an important processing strategy of the nervous system' [cite key=olshausen2004sparse]. But it remains a hypothesis since doubt can still be cast: the evidence may not actually support sparsity, since most experiments are performed using anaesthetised animals that may be the cause of any observed sparsity; or the appropriate stimuli needed to fully drive the neurons under study are simply not being used. Many papers provide a deeper theoretical and experimental understanding of sparse coding, some of which are:
- Sparse coding of sensory inputs, B. A. Olshausen and D. J. Field
- Experimental evidence for sparse firing in the neocortex, A. L. Barth and J. F. A. Poulet
- Sparse coding in the primate cortex, P. Földiák
The diversity of sensory inputs has led us to establish a computational problem of efficiently representing sensory data. One algorithmic solution to this problem forms an efficient sensory representation—efficient for energy use, memory and decision making—by representing and manipulating information through sparse and overcomplete neural codes. This is a solution that is implemented in brains by the sparse firing of neurons, and in regions throughout the brain. This strategy can also used by machines.
Sparse Machine Learning
[dropcap]Sparsity[/dropcap] highlights the important role that zeros play in computation. In machine learning, we manipulate vectors, and we can distinguish between two types of sparse vectors based on how zero is treated. A strongly sparse vector has a few elements with large values, but the majority are exactly zero. A weakly sparse vector has a few elements with large values and all other elements with values close to zero [cite key=mohamed2011bayesian]. Mirroring the advantages of sparsity in the brain, sparsity in either form allows us to:
- Capture implicit statistical structure in many data sources,
- Better interpret our data,
- Perform feature selection and regularisation,
- Deal with high-dimensional data,
- Reduce computational costs,
- Compress our data and provide guarantees on the accuracy of its recovery.
Sparsity is a constraint we impose on the models we use to explain our data. To explore this further, consider a generic model of observed data
![]()
that uses some context
![]()
and parameters
![]()
. Your favourite model can be described this way, e.g., for classification,
![]()
is the label and
![]()
the observed features or covariates. There are many ways to represent a model, but one of the most flexible is to provide a probabilistic specification:
![]()
where
![]()
is a scoring or likelihood function, which is a Gaussian distribution for linear regression, or a Bernoulli distribution for logistic regression. Because this specification is generic, we can easily think of more expressive regression models such as recursive generalised linear models/deep networks or density estimators. If we follow the maximum likelihood principle, we obtain a penalised maximum likelihood learning objective
![]()
, which maximises the log joint-probability distribution:
![]()
This objective tells us that to exploit the power of sparsity in our model, we must restrict the types of probability distributions
![]()
, or the penalties
![]()
, that are used. For a vector
![]()
, the simplest measure of its sparsity is to count the number of non-zero entries. This can be achieved using the
![]()
(quasi-) norm:
![Rendered by QuickLaTeX.com \[ \|\boldsymbol{\theta}\|_0 = \sum_{d = 1}^{D} \theta_d \neq 0)\]](https://blog.shakirm.com/wp-content/ql-cache/quicklatex.com-83191530bfb878360ac84151480e6dd1_l3.png)
where D is the dimensionality of the vector. The
![]()
-norm embodies strong sparsity, but leads to difficult combinatorial problems that are hard to deal with when used as the penalty function within our learning objective. Instead
![]()
-norms are used, which are smooth relaxations, that reflect weak-sparse reasoning when
![]()
:
![Rendered by QuickLaTeX.com \[ \|\boldsymbol{\theta}\|_p = \left( \sum_{d = 1}^{D} |\theta_d|^p \right)^{1/p}\]](https://blog.shakirm.com/wp-content/ql-cache/quicklatex.com-da8c5b413bf0e6d09a5036da54ba3490_l3.png)
The case when
![]()
is important since this is the closest convex relaxation of the
![]()
norm. When we maximise the loss function
![]()
using the
![]()
norms as penalties
![]()
, we are led to solutions that have few non-zero elements, and thus to sparse solutions.
If we think about these penalties in terms of the distributions
![]()
they correspond to, we find that they are log-transforms of distributions of the form:
![]()
Such distributions are sparsity-promoting distributions; when p =1, this is the Laplace distribution. This connection lays a path towards a rich new source of sparsity-promoting distributions, since the Laplace distribution can also be written as a specific instance of a the more general class of Gaussian scale-mixture distributions [cite key=west1987scale], defined as:
![]()
where
![]()
is the Gaussian mean, the Gaussian variance consists of a local component
![]()
and a global component
![]()
,
![]()
is a positive function,
![]()
is a mixing density on
![]()
. To derive the Laplace distribution, an Exponential mixing density is used.
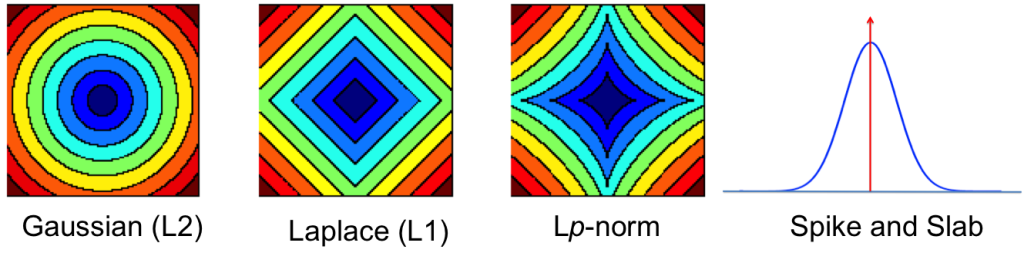
This mixture distribution allows us to provide a more concrete characterisation of sparsity-promoting distributions: distributions that are peaked at zero with heavy tails that decay at a polynomial rate (i.e. decay according to some power law, or have high-excess kurtosis) [cite key=johnstone2004needles]. By changing the mixing density we obtain a wide variety of (weak) sparsity-promoting distributions [cite key=polson2010shrink]. The idea of a mixture distribution can also be used to form distributions that allow for strong sparsity, i.e. a spike-and-slab distribution: a mixture of a delta distribution at zero (a spike) and any other continuous distribution (the slab). And as is often the case, strong and weak sparsity can be unified by characterising them as Levy processes [cite key=polson2010shrink]. And while we won't discuss this here, sparsity can also be indirectly induced by overcomplete and non-negative representations.
A machine learning solution to a problem requires three ingredients: a model, a learning objective and an algorithm. We explored a generic model that introduced sparse reasoning by incorporating sparsity-promoting distributions. Penalised maximum likelihood is one poplar learning objective that we explored, although many other learning objectives can be used instead, including majorisation-minimisation methods (like expectation-maximisation) and Bayesian posterior inference. This post has not explored the algorithms that solve our learning objectives, but many different algorithms are possible, including sub-gradient methods, least-angle regression, shrinkage-thresholding algorithms, Metropolis-Hastings sampling, and many others.
The following reviews and papers provide a broad exploration of sparse learning, and show the many applications to which sparsity has contributed.
- Sparse Modeling for Image and Vision Processing. Mairal, Bach, Ponce.
- An introduction to compressive sampling. Candes and Wakin.
- Shrink Globally, Act Locally: Sparse Bayesian Regularization and Prediction. Polson and Scott
- Bayesian and L1 approaches for sparse unsupervised learning. Mohamed, Heller, Ghahramani
- Learning the parts of objects by non-negative matrix factorization, Lee and Seung
Final Words
Sparsity is a strategy for efficient information representation that is successfully exploited by both brains and machines. The connections between computational and biological learning using sparsity have only been lightly made, leaving much opportunity for these learning paradigms to be better connected. But even with such limited association, the understanding we do have is an important source of inspiration, and helps clear our path towards a richer understanding of both computational and biological learning.
[bibsource file=http://www.shakirm.com/blog-bib/brainsMachines/sparsity.bib]
3 thoughts on “Learning in Brains and Machines (2): The Dogma of Sparsity”