Our ability to rewrite statistical problems in an equivalent but different form, to reparameterise them, is one of the most general-purpose tools we have in mathematical statistics. We used reparameterisation in all the tricks we explored in this series so far: trick 1 re-expressed a log-partition function in terms of copies (replicas) of the marginal probability, trick 2 re-expressed a binary MRF as an undirected model with Gaussian latent variables, and trick 3 re-expressed the computation of the matrix trace using a randomised form. Such reparameterisations allow us to use different tools for computation, give us a new understanding and approach for analysis, and better expose the connections to related research areas.
Today's trick will focus on one subset of reparameterisation methods, ones we shall refer to as random variate reparameterisations: the substitution of a random variable by a deterministic transformation of a simpler random variable. Machine learning is filled to the brim with random variables, so we'll find many applications of today's trick, including problems in Monte Carlo sampling and stochastic optimisation.
One-liners
To develop the class of random variate reparameterisations, we will first need to develop the tricks that they themselves rely on: the methods by which non-uniform random numbers, or random variates, can be generated. The most popular methods are the one-liners, which give us the simple tools to generate random variates in one line of code, following the classic paper by Luc Devroye of the same title [cite key=devroye1996random].
Imagine water flowing through a series of pipes: one-line transformations specify a path 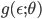 through which samples
through which samples 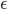 from an initial base distribution flow, ultimately forming a sample from a desired distribution
from an initial base distribution flow, ultimately forming a sample from a desired distribution 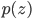 . To be a one-liner, the transformation
. To be a one-liner, the transformation 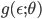 must be composed of primitive functions (arithmetic operations, log, exp, cos) and the base distribution
must be composed of primitive functions (arithmetic operations, log, exp, cos) and the base distribution 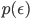 must be easy to sample from. The transformations, our system of pipes, can be designed in a number of ways. Three popular approaches are:
must be easy to sample from. The transformations, our system of pipes, can be designed in a number of ways. Three popular approaches are:
- Inversion methods. To generate a sample from a distribution
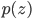 , we can use the inverse cumulative distribution function (CDF) as our transformation, if it is known and invertible, with uniform random numbers as the base distribution. Many of the distributions we use every day are in this category, so this is a popular default approach.
, we can use the inverse cumulative distribution function (CDF) as our transformation, if it is known and invertible, with uniform random numbers as the base distribution. Many of the distributions we use every day are in this category, so this is a popular default approach. - Polar methods. Sometimes it is more convenient to think of generating a pair of random variates
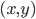 from the target distribution
from the target distribution 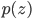 . We can map this pair to a representation in polar form
. We can map this pair to a representation in polar form 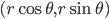 , which exposes other mechanisms for sampling, e.g., the famous Box-Muller transform is derived in this way.
, which exposes other mechanisms for sampling, e.g., the famous Box-Muller transform is derived in this way. - Co-ordinate transformation methods. Many co-ordinate transformations exist that allow us to transform one distribution into another form, e.g., using additive or multiplicative location-scale transformations. This will be our default approach since co-ordinate transformations allow for easy reparameterisation of a diverse and flexible class of distributions.
Using this reasoning, you can easily see that the transformations in the table below can be implemented in one line of code; many of the sampling algorithms in our software tools, such as Randomkit used in numpy and torch-distributions, use one-liners. Because generating random numbers is so fundamental, we inevitably have many names for this reasoning, including as non-uniform generators [cite key='devroye1986non'], as simple instances of normalising flows, and as one-liners (and their extended forms).
[table]
Target, 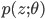 , Base
, Base 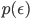 , One-liner
, One-liner 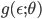
Exponential, 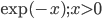 ,
, 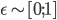 ,
, 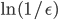
Cauchy, 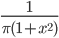 ,
,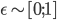 ,
, 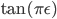
Laplace, 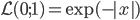 ,
, 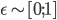
, 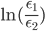
Laplace, 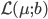 ,
, 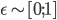
, 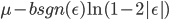
Std Gaussian, 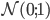 ,
,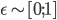
, 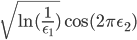
Gaussian, 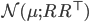 ,
, 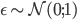 ,
, 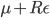
Rademacher, 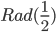 ,
, 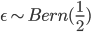 ,
, 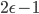
Log-Normal, 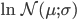 ,
, 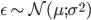 ,
, 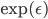
Inv Gamma, 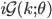 ,
, 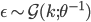 ,
, 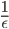
[/table]
The point of describing these one-liners is that when we see a random variable z, we can often explore the implications of using random variate reparameterisation by replacing z with the function 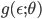 . In Monte Carlo sampling, this approach is sometimes known as a non-centred parameterisation [cite key=papaspiliopoulos2007general], which can lead to more efficient mixing of the Markov chain. Another important application of random variate reparameterisation is in stochastic optimisation, which we explore next.
. In Monte Carlo sampling, this approach is sometimes known as a non-centred parameterisation [cite key=papaspiliopoulos2007general], which can lead to more efficient mixing of the Markov chain. Another important application of random variate reparameterisation is in stochastic optimisation, which we explore next.
Reparameterisation for Stochastic Optimisation
One oft-encountered problem is computing the gradient of an expectation of a smooth function f:
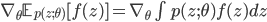
This is a recurring task in machine learning, needed for posterior computation in variational inference, value function and policy learning in reinforcement learning, derivative pricing in computational finance, and inventory control in operations research, amongst many others. This gradient is often difficult to compute because the integral is typically unknown and the parameters 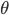 , with respect to which we are computing the gradient, are of the distribution
, with respect to which we are computing the gradient, are of the distribution 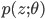 . But where a random variable z appears we can try our random variable reparameterisation trick, which in this case allows us to compute the gradient in a more amenable way:
. But where a random variable z appears we can try our random variable reparameterisation trick, which in this case allows us to compute the gradient in a more amenable way:
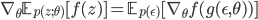
Let's derive this expression and explore the implications of it for our optimisation problem. One-liners give us a transformation from a distribution 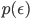 to another
to another 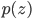 , thus the differential area (mass of the distribution) is invariant under the change of variables. This property implies that:
, thus the differential area (mass of the distribution) is invariant under the change of variables. This property implies that:
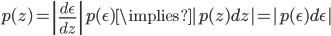
Re-expressing the troublesome stochastic optimisation problem using random variate reparameterisation, we find:
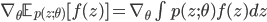
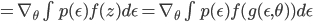
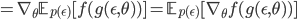
In the second line, we reparameterised our random variable in terms of a one-line generating mechanism. In the final line, the gradient is now unrelated to the distribution with which we take the expectation, so easily passes through the integral. Our assumptions throughout this process were simple: 1) the use of a continuous random variable z with a known one-line reparameterisation, 2) the ability to easily generate samples 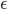 from the base distribution, and 3) a differentiable function f.
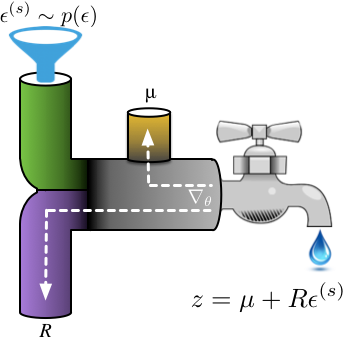
from the base distribution, and 3) a differentiable function f.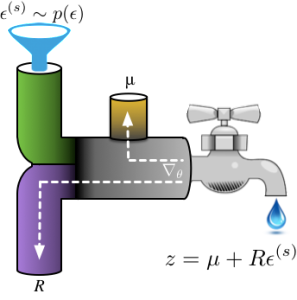
Using reparameterisation has given us a new approach for optimisation: we can obtain an unbiased estimator of the gradient by computing the expectation by Monte Carlo integration. Using the water-pipes analogy, once samples of 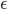 are available, they flow through the path specified by the transformation to produce random variates. Gradients flow backwards through this path, allowing for computation by automatic differentiation and composition with other gradient-based systems.
are available, they flow through the path specified by the transformation to produce random variates. Gradients flow backwards through this path, allowing for computation by automatic differentiation and composition with other gradient-based systems.
As with the one-liners, this approach appears under many different names:
- Perturbation analysis and pathwise derivatives. In stochastic optimisation, the reparameterised gradient estimator appears under the heading of perturbation analysis [cite key= fu2006gradient]. Much of the initial work used a reparamaterisation using one-liners based on the inversion method. The resulting estimators are sometimes called pathwise derivative (PD) estimators [cite key=glasserman2003monte]. The works by Fu, and Glasserman are comprehensive references using this perspective.
- Stochastic Gradient Estimation, M. Fu.
- Gradient estimation via Perturbation analysis, P. Glasserman, Springer, 1991.
- Stochastic backpropagation. There are a number of recent uses of random variate reparameterisation in machine learning to develop scalable variational inference in deep generative models and Gaussian processes. At least three papers concurrently explored this approach:
- Stochastic Backpropagation and Approximate Inference in Deep Generative Models
- Random variate reparameterisation is one consequence of the technique described as stochastic backpropagation in this paper [cite key=rezende2014stochastic]. There also are other ways to derive unbiased gradient estimators and this paper discusses this aspect and provides some simple variance analysis.
- Auto-Encoding Variational Bayes
- We can attribute the popularity of the expression 'reparameterisation trick' to this paper [cite key=kingma2014auto], which provides a clear description of the trick and the range of transformations available.
- Doubly Stochastic Variational Bayes for non-Conjugate Inference
- Stochastic Backpropagation and Approximate Inference in Deep Generative Models
- Affine-independent inference.
Since we obtain a Monte Carlo estimator, there are now important questions to ask about the variance of the estimator. Being pathwise gradients (i.e. they implement the chain-rule), these estimators provide an implicit tracking of dependencies between parameters—a provenance tracking—which contributes to the low variance. Gradient estimators based on this approach often have the lowest variance amongst competing approaches. We can also think about ways in which reparameterisation might allow for efficient computation of higher-order gradients. This stochastic optimisation problem can be solved in another very different way and our next trick, the log-derivative trick, will continue this theme and explore these aspects further.
Summary
Random variate reparameterisation is a tool by which we substitute random variables of some known distribution by a deterministic transformation of another random variable. One of the underlying tools that provide us with the deterministic transformations that are needed to achieve this, are the one-liners. Armed with these tricks, we can develop alternative approaches to often-encountered machine learning problems, resulting in faster mixing Markov chains, or scalable Monte Carlo gradient estimators. These methods remain simple and easy to implement, and is what cements their popularity as a tool for developing accurate and scalable machine learning systems.
[bibsource file=http://www.shakirm.com/blog-bib/trickOfTheDay/oneliners.bib]
Awesome post! Quick note: the one-liner for a standard Gaussian should be sqrt(2 * ln(1/eps_1) * cos(2 * pi * eps_2)
see : https://en.wikipedia.org/wiki/Box%E2%80%93Muller_transform
Fabulous introduction on the reparametrization tricks! Will keep learning from you blog and presumably will get tremendous abundance of knowledge. Just a little confusing about the variable transformation part, according to the introduction on the Wiki link you posted, the implication arrow between p(ϵ)|dϵ|=p(z)|dz| and p(z)=∣dϵ/dz∣p(ϵ) the other term should be perhaps the other way around. Please correct me if i've made mistakes, but following from the measure theory the measure of dz, i.e. p(z), should be 'preserved' under the inverse mapping f^-1: z->ϵ, so that p(ϵ)|dϵ|=p(z)|dz|, then the LHS equation can be implied. Thank you again for your posting and wish i may contribute to the work a little, too.
Thanks a bunch! One question: is the reparametrization trick restricted to transformations where the Jacobian is diagonal? I'm just asking because you took |d eps / dz | apart as if it was.
GREAT article, thanks!
Hi!
Very nice article, it makes for a nice read and explains some basic concepts. I have a question though. Somewhere you say that the vanilla gradient is hard to compute because
"This gradient is often difficult to compute because the integral is typically unknown and the parameters θ, with respect to which we are computing the gradient, are of the distribution p(z;θ)p(z;θ)."
I recognize the first difficulty. Indeed, if your function f() is complicated, like a neural network, computing analytically the integral is hard.
However, what do you mean exactly by the second difficulty? Do you mean that because the variable θ with respect to which you take the gradient is also in the pdf, makes the gradient computation much harder, because the overall composite function becomes harder?
Or because now you need to take the expectation over a multi-dimensional random variable, whereas after the reparameterization trick the expectation is taken over the single dimensional ε? Which implies that you need much fewer samples to compute a good enough expectation, which in turn implies that you can much less variance (or smaller bias) of the estimator?
Thanks Shakir for great posts, please keep doing this.